• 1. BB平台 测验
  • 第 1-4 学时测验
  • 第 5-8 学时测验
  • 第 9-12 学时测验
  • 第 13-16 学时测验
  • 第 17-20 学时测验
  • 第 21-24 学时测验
  • 第 25-28 学时测验
  • 第 29-32 学时测验
  • 第 33-36 学时测验
  • 第 37-40 学时测验
  • 第 41-44 学时测验
  • 第 45-48 学时测验
• 2. 线上期末考试题

1. BB平台 测验

第 1-4 学时测验

1. 若 $P$ ，$Q$ 为两个命题，$P \rightarrow Q$ 真值为 $F$，当且仅当 $P$ 为 [ $T$ ] ，$Q$ 为 [ $F$ ] 。
2. 设 $P$ ，$Q$ 的真值为 $0$，$R$，$S$的真值为 $1$，则 $\neg(P \vee(Q \rightarrow(R \wedge \neg P))) \rightarrow(R \vee \neg S)$ 的真值 $=$ [1]
3. 令 $P$ ：今天下雨了，$Q$ ：我没带伞，则命题“虽然今天下雨了，但是我没带伞”可符号化为 [ $P \wedge Q$ ] 。
4. $P$ : 你努力, $Q$ : 你失败。“除非你努力, 否则你将失败”可符号化为 [ $\neg \mathrm{P} \rightarrow \mathrm{Q}$ ]。
5. 令 $P$ :上午下雨。$Q$ :我去看电影。 $R$ :我在家里读书。$S$ :我在家里看报。假如上午不下雨，我去看电影，否则就在家里读书或看报。其符号化表达式为 [ $(\neg \mathrm{P} \rightarrow \mathrm{Q}) \wedge(\mathrm{P} \rightarrow(\mathrm{R} \bar{\vee} \mathrm{S}))$ ]。

第 5-8 学时测验

1. 命题公式 $\neg(P \rightarrow Q)$ 的主析取范式是 [ $\mathrm{P} \wedge \neg \mathrm{Q}$ ]。
2. $(\neg \mathrm{A} \rightarrow(\mathrm{D} \wedge \mathrm{E})) \wedge(\mathrm{B} \vee \mathrm{C}) \wedge((\mathrm{B} \vee \mathrm{C}) \rightarrow \neg \mathrm{A}) \Rightarrow \mathrm{D} \wedge \mathrm{E}$ 是永真蕴含式。 [对]
3. 含有三个命题变元 $P$ , $Q$ , $R$ 的命题公式 $P∧Q$ 的主析取范式是 [ $(P∧Q∧R)∨( P∧Q∧¬R)$ ]
4. 设命题公式 $G ： \neg P \rightarrow(Q \wedge R)$ ，则使公式G取真值为1的 $P ， Q ， R$ 赋值分别是 [ 0,1,1; 1,0,0 ] (2个答案)
5. 下列等价式成立的是 [ $P \rightarrow(Q \rightarrow P) \Leftrightarrow \neg P \rightarrow(P \rightarrow \neg Q)$ ]

第 9-12 学时测验

网站不显示已提交答案

第 13-16 学时测验

网站不显示已提交答案

第 17-20 学时测验

1. 下列公式中不正确的是 [ $\exists x(P(x) \wedge Q(x)) \Leftrightarrow \exists x P(x) \wedge \exists x Q(x)$ ]

2. 谓词公式 $\exists x F(x, y) \rightarrow \forall x(G(x) \wedge H(x, y))$ 的前束析取范式是 [ $\forall z \forall x(\neg F(z, y) \vee(G(x) \wedge H(x, y))$ ]

3. 下列推理片段正确的是 [ (1) $∃x∀yA(x,y)$ $P$ ; (2) $∀yA(c,y)$ $ES (1)$ ]

4. 试用谓词推理理论验证下述陈述的有效性，并分析给出的推导过程是否有错，若有错填写出错步骤号，无错填"无"。

   每个考生或者勤奋或者聪明，所有勤奋的人都将有所作为，但并非所有考生都将有所作为，所以，一定有些考生是聪明的。

   符号化：$P(e)$ : $e$ 是考生；$Q (e)$ : $e$ 将有所作为；$A(e)$ : $e$ 是勤奋的；$B(e)$ : $e$ 是聪明的。论域：人的集合。

   $\forall x(P(x) \rightarrow(A(x) \vee B(x))), \forall x(A(x) \rightarrow \mathrm{Q}(x)), \neg \forall x(P(x) \rightarrow Q(x)) \Rightarrow \exists x(P(x) \wedge B(x))$
   (1) $\neg \forall \mathrm{x}(\mathrm{P}(\mathrm{x}) \rightarrow \mathrm{Q}(\mathrm{x})) \quad \mathrm{P}$
   (2) $\exists x \neg(P(x) \rightarrow Q(x)) \quad T(1) \quad E$
   (3) $\exists x \neg(\neg P(x) \vee Q(x)) \quad T(2) \quad E$
   (4) $\exists x(P(x) \wedge \neg Q(x)) \quad T(3) \quad E$
   (5) $\mathrm{P}(\mathrm{a}) \wedge \neg \mathrm{Q}(\mathrm{a}) \quad \mathrm{ES} \quad$ (4)
   (6) $P(a) \quad T(5) \quad I$
   (7) $\forall x(P(x) \rightarrow(A(x) \vee B(x))) \quad P$
   (8) $P(a) \rightarrow(A(a) \vee B(a)) \quad US \quad$ (7)
   (9) $A(a) \vee B(a) \quad T \quad(6)(8) \quad I$
   (10) $\forall \mathrm{x}(\mathrm{A}(\mathrm{x}) \rightarrow \mathrm{Q}(\mathrm{x})) \quad \mathrm{P}$
   (11) $A(a) \rightarrow Q(a) \quad US \quad(10)$
   (12) $\neg Q(a) \quad T \quad (5) \quad I$
   (13) $\neg A(a) \quad T \quad(11)(12) \quad I$
   (14) $B(a) \quad \mathrm{T} \quad(9)(13) \quad I$
   (15) $P(a) \wedge B(a) \quad T \quad(6)(14) \quad I$
   (16) $\exists x(P(x) \wedge B(x)) \quad E G$

   [无]

5. 设 $P(x, y)$ 为 $x$ 整除 $y ， Q(x)$ 为 $x<2$ ，个体域为 $\{1,2\}$ ，则公式 $\forall x \exists y(P(x, y) \rightarrow Q(x))$ 的真值是 [真]

第 21-24 学时测验

1. 设 $S=\{\Phi,\{1\},\{1,2\}\}$ ，则 $2^s$ 有 [8] 个元素。
2. 设 $A=\Phi, B=\{\Phi,\{\Phi\}\}$ ，则 $B - A$ 是 [$\{\Phi,\{\Phi\}\}$]
3. 设 $A=\{2 ， a ，\{3\} ， 4\} ， B=\{\{a\} ， 3 ， 4 ， 1\}$ ，请在下列每对集合中填入适当的符号: $\in ， \subseteq$ 。
   (1) $\{a\}[\in] B$
   (2) $\{a, 4,\{3\}\}[\subseteq] A$
4. 设 $A=\{1 ， 2\} ， B=\{a\}$ ，则 $2^{A} \cup 2^{B}=2^{A \cup B}$ 。（其中 $2^{A}$ 为 $\mathrm{P}(A)$ ）[错]
5. 120个学生参加考试，这次考试有 $A$ , $B$ 和 $C$ 共3道题，考试结果如下：12个学生3道题都做对了；20个学生做对了 $A$ 题与 $B$ 题；16个学生做对了 $A$ 题与 $C$ 题；28个学生做对了 $B$ 题与 $C$ 题；做对了 $A$ 题的有48个学生；做对 $B$ 题的有56个学生；还有16个学生一道题也没做对。则做对 $C$ 题的学生有 [52] 个。

第 25-28 学时测验

1. 非空集合A上的空关系不具备的性质是 [自反性] 。
2. 假设 $A={a,b,c,d}$ ，则有 [$2^{16}$] 种集合A上的不同二元关系。
3. 设R是集合A上的二元关系，$I_A$ 是 $A$ 上的恒等关系，如果 $R⊂I_A$ ，则下面四个命题中为真的是 [ $R$ 不是自反的] 。
4. 假设 $A={a,b,c}$ ，A上的关系 $R=\{<a,b>,<a,c>\}$ ，那么关系R具有 [反自反性、反对称性、传递性] 。
5. 设集合 $A={0, a}, B={0,a,1}$ ,则 $A∪B$ 上的恒等关系是 [$\{<0,0>,<a,a>,<1,1>\}$] 。

第 29-32 学时测验

1. 设 $R，S$ 是集合 $A$ 上的关系，则下列说法正确的是 [若 $R、S$ 自反，则 $R \circ S$ 也自反] 。
2. 令R和S都是人类上的关系，且 $R=\{<x,y>|x是y的父亲\}$ ， $S={<x,y>|x是y的母亲} $，则 $<x,y>∈R\circ S^C$ 表示 $x$ 是 $y$ 的 [丈夫] 。
3. $X$ 是集合，且 $|X|=4$ ，则 $X$ 上有 [15] 个不同的等价关系。
4. 设 $A=\{0，1\}$，$B=\{1，2，3\}$ ，则 $|A×B| = 2^3$ 。 [错]
5. $A=\{1，2，3，4，5，6\}$，A上二元关系 $T= \{ <x,y>| x÷y 是素数 \}$ ，则 $T$ 具有 [反对称性、反自反性] 性质。

第 33-36 学时测验

1. 设 $\{a,b,c\}$ 上的偏序关系 $(P(A), ⊆)$ ，则 $P(A)$ 的子集 $B=\{Φ,\{a\},\{b\},\{a,b\},\{b,c\}\}$的极大元是 [$\{a,b\},\{b,c\}$] , 最大元是 [无] , 上届是 [$\{a,b,c\}$] , 下确界是 [$Φ$] 。

2. 设 $\mathrm{R}, \mathrm{S}$ 是 $\mathrm{A}=\{1,2,3,4\}$ 上的等价关系, 其关系矩阵分别为

   $M_{R}=\left[\begin{array}{cccc} 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right], \quad M_{S}=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]$

   则包含 $\mathrm{R}$ 与 $\mathrm{S}$ 的最小的等价关系为 [$\left[\begin{array}{llll}1 & 1 & 1 & 0 \\1 & 1 & 1 & 0 \\1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]$] 。

3. 若集合 $A=\{1,2,3,4,5\}$ 上的等价关系 $R=\{<1,1>,<2,2>,<3,3>,<4,4>,<5,5><1,2><2,1>,<3,4>,<4,3>\}$ ，则商集 $A/R$ 为 [$\{\{1,2\}, \{3,4\},\{5\}\}$] 。

4. $R$ 为集合 $A = \{1,2,3,4,5\}$ 上的等价关系，已知商集 $A/R=\{\{1,2\},\{3\},\{4,5\}\}$ ，则关系 $R$ 为 [$\mathrm{I}_{\mathrm{A}} \cup\{<1,2>,<2,1>,<4,5>,<5,4>\}$] 。

5. 集合 $A=\{1,2,3,4,5,6,7\}$ 上的一个相容关系 $R$ 如图所示，其最大相容类 $C_R(A)$ 为 [$\{\{1,2,5\},\{1,3,5\},\{3,4\},\{4,6\}\}$]

   

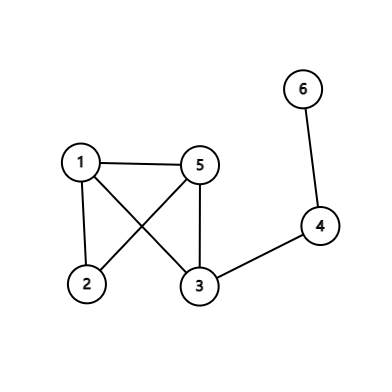
第 37-40 学时测验

1. 设 $A=\{a,b,c\}, B=\{1,2,3\}$ ，则下列关系中能构成 $A$ 到 $B$ 函数的是 [$f_3=\{<a,1>,<b,1>,<c,1>\}$] 。
2. 设函数 $f: B→C$ ，$g: A→B$ 都是单射，则 $f°g: A→C$ [是单射]
3. 设A是有穷集，$|A|=5$ ， $A$ 上有 [52] 种不同的等价关系，从 $A$ 到 $A$ 的不同双射函数有 [120] 个。
4. 设 $|X|=3$ , $|Y|=2$ ,则从 $X$ 到 $Y$ 可以生成不同的满射个数为 [6] 。
5. 设 $A=\{2,3,4\}$ , $B =\{2,4,7,10,12\}$ ,从 $A$ 到 $B$ 的关系 $R=\{<a,b>|a∈A, b∈B,且a整除b\}$ ,则关系 $R$ [不是] 函数，其逆关系 [不是] 函数。

第 41-44 学时测验

1. 图 $G$ 有21条边，3个4度结点，其余均为3度结点，则 $G$ 有 [13] 个结点。

2. 含5个结点，4条边的无向连通图（不同构）有 [3] 个。

3. 设图 $G = < V，E >$ ，$V={V1，V2，V3，V4} $，邻接矩阵 $A=\left(\begin{array}{llll}0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0\end{array}\right)$ ，则 $V1$ 的入度 $=$ [3]，从 $V2$ 到 $V1$ 的长度为2的路有 [2] 条。

4. 已知下图，它的点连通度为 [1] ，边连通度为 [1] 。

   

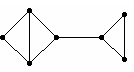
5. 下面四组数能构成无向简单图的度数列的有 [1,2,2,3,4] 。

第 45-48 学时测验

1. 设 $G$ 是一个哈密尔顿图，则 $G$ 一定是 [连通图] 。

2. 下图 [不是] 平面图。

   

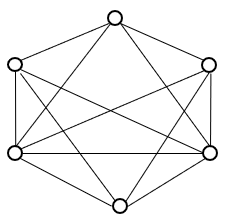
3. 若简单连通平面图 $G$ 有4个节点，3个面，则 $G$ 有 [5] 条边。

4. 二部图 $K3,3$ 是 [哈密尔顿图] 。

5. 下面图中既是欧拉图又是哈密尔顿图的是 [ ] 。

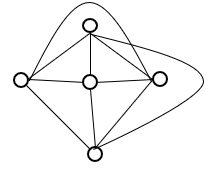2. 线上期末考试题

1. 已知某芯片有三项输入 $(P、Q、R)$ ，经测试其输入输出关系如表所示。

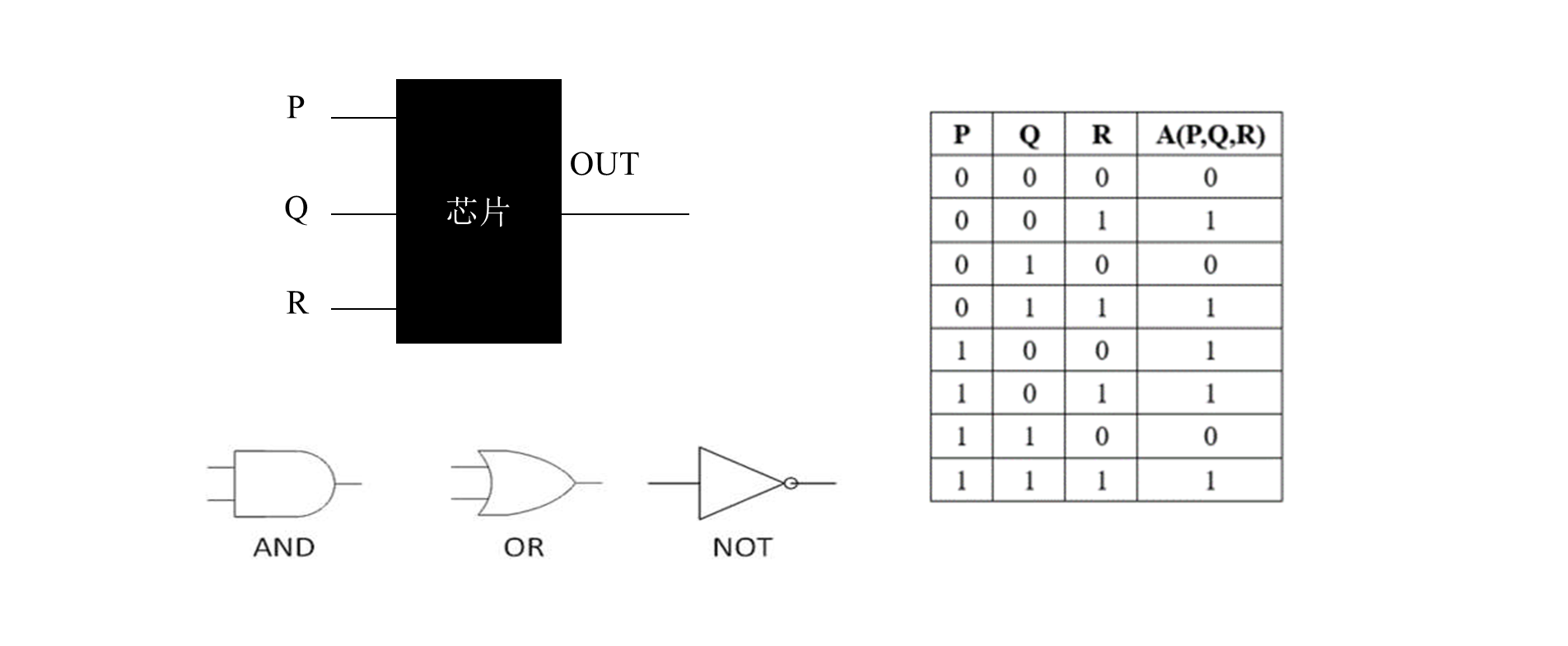
（1）请写出 $A(P,Q,R)$ 的主析取范式。（10分）

（2）使用图中给出的与、或、非逻辑电路元件，以主合取范式为依据，画出该芯片的内部逻辑电路结构。（10分）

（3）请通过对 $A(P,Q,R)$ 进行化简，画出以析取 $Ú$ 为树根的 $A(P,Q,R)$ 的根树表述。（10分）

2. 定义：若 $R$ 是A上的关系， $R'$ 是包含R的最小的等价关系（自反，对称，传递），则称 $R'$ 为关系 $R$ 的等价闭包。已知 $A=\{1, 2, 3, 4, 5，6，7，8\}$ , A上的关系 $R=\{<1,2>,<1,5>,<1,4>,<2,3>,<2,4>,<3,1>,<4,3>,<4,5>,<5,2>，<5,3>,<6，6>,<7,7>,<6,8>\}$ 。

   （1）画出 $R$ 的有向图表示，求R的可达矩阵 $P$ 。（10分）

   （2）证明 $R$ 的有向图（忽略边的方向）是非平面图。（10分）

   （3）求R的等价闭包 $R'$ 的有向图， $R'$ 的矩阵表示。要求描述求解过程。（20分）

   （4）求 $A/R'$ 。 （10分）

3. 请分析“fight the coronavirus pandemic”中每个字符的频率，按字符频率画出字符的哈夫曼树表示，并给出每个字符的前缀码。（20分）

   注意：字符按照词频排序，词频相同的字符按照字母表顺序排序。新生成的父节点权值若与字符叶子权值相同，则叶子在左、父节点在右。