1. 问题提出

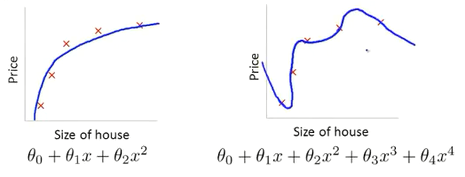
对于房子的大小和房价的关系，如果我们使用一个二次函数来拟合（下图左侧），会得到一个相当不错的拟合结果。但是当使用较高阶的多项式来拟合（下图右侧），会得到一个非常拟合数据的曲线，但是已经过拟合，并不能泛化到更多的数据上。

此时，优化的目标函数为：

min⁡θ12m∑i=1m(hθ(x(i))−y(i))2)\min_\theta{\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2)}

2. 解决方法

如果我们在上边的函数中加入两个惩罚项：

min⁡θ12m∑i=1m(hθ(x(i))−y(i))2)+1000⋅θ32+1000⋅θ42\min_\theta{\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2)+1000\cdot\theta_3^2+1000\cdot\theta_4^2}

1000只是一个较大的数，此时要想使整个函数能够取到最小值，就要尽量使 θ3\theta_3 和 θ4\theta_4 取到的值变小，也就是使 θ3\theta_3 和 θ4\theta_4 接近0，就相当于淡化四次函数中，θ3x3\theta_3x^3 和 θ4x4\theta_4x^4 项的效果，使其偏向于一个二次方程，最终的拟合效果会更好。

3. 正则化思想

如果参数 θ0,θ1,…,θn\theta_{0}, \theta_{1}, \ldots, \theta_{n} 的值比较小，意味着一个更简单的假设模型。在上边的例子中，我们给 θ3\theta_3 和 θ4\theta_4 加了惩罚项，当它们都接近0时，会得到一个更简单的假设模型，就相当于一个二次函数。如果把所有的参数都加上惩罚函数，就相当于尽量去简化这个假设模型。结果表明，参数的值越小，我们得到的函数就会越平滑，因此也更不容易出现过拟合。

所以，更小的 θ0,θ1,…,θn\theta_{0}, \theta_{1}, \ldots, \theta_{n} ，意味着：

  • “更简单”的假设模型
  • 更不容易过拟合

4. 例子

对于一个房价的预测模型：

  • 可能存在特征：x1,x2,…,x100x_{1}, x_{2}, \ldots, x_{100}
  • 对应的参数：θ0,θ1,θ2,…,θ100\theta_{0}, \theta_{1}, \theta_{2}, \ldots, \theta_{100}

模型的代价函数为：

J(θ)=12m∑i=1m(hθ(x(i))−y(i))2J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2

我们并不知道哪些特征是高阶项，所以我们对代价函数的每个特征都加上正则化项：

J(θ)=12m[∑i=1m(hθ(x(i))−y(i))2+λ∑j=1mθj2]J(\theta)=\frac{1}{2m}\left[\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{j=1}^{m}\theta^2_j\right]

其中，jj 从1开始， θ0\theta_0 并没有出现在正则化项中，不过有没有 θ0\theta_0 最终的效果差距并不大； λ\lambda 为正则化参数，来控制两个目标间的取舍：

  • 更好的拟合训练集
  • 使参数尽量小，避免出现过拟合

如果 λ\lambda 的值过大，那么最后得到的所有参数都会接近于0，就相当于把函数的所有项都忽略了，最后只剩下 θ0\theta_0 ，就相当于最后预测的房价直接等于 θ0\theta_0 ，也就相当于用一条直线去拟合函数，这样偏差过大。所以为了正则化更好的起作用，我们就要去选择一个合适的 λ\lambda 值。